定理证明¶

相等性¶

Idris 可以声明命题的相等性，陈述并证明有关程序的定理。相等性是内建的，不过这里给出其概念上的定义：

data (=) : a -> b -> Type where
   Refl : x = x

任何类型的任何值之间都可以判断相等性，然而构造相等性证明的唯一方式就是值确实相等。例如：

fiveIsFive : 5 = 5
fiveIsFive = Refl

twoPlusTwo : 2 + 2 = 4
twoPlusTwo = Refl

空类型¶

存在一个空类型 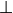$\bot$ ，它没有构造器。因此，在不使用部分定义或一般递归函数的情况下，无法构造出空类型的元素（详见完全性检查一节）。由此，我们可以用空类型来证明某些命题是不可能的，例如零不可能是任何自然数的后继：

disjoint : (n : Nat) -> Z = S n -> Void
disjoint n p = replace {P = disjointTy} p ()
  where
    disjointTy : Nat -> Type
    disjointTy Z = ()
    disjointTy (S k) = Void

我们不必太关心该函数如何工作 — 本质上，它应用库函数 replace，根据相等证明来变换谓词。在本例中，我们利用某些东西无法存在的证明，将一个可以存在的类型（即空元组）的值，变换成了一个无法存在的类型的值。

一旦拥有了空类型的元素，我们就能证明任何东西。void 在库中定义，用于辅助反证法。

void : Void -> a

简单定理¶

当对依赖类型进行类型检查时，该类型就会被 规范化（Normalized）。比如我们想要证明以下关于 plus 的归约行为（Reduction Behaviour）的定理：

plusReduces : (n:Nat) -> plus Z n = n

我们将该定理的陈述写成了类型，就像写出程序的类型一样。实际上证明和程序之间并没有本质的区别。就我们所关注的而言，证明不过是个程序，只是它的类型精确到足以保证满足我们关心的特殊性质。

我们不会在这里深入细节，Curry-Howard 同构 [1] 解释了这种关系。该证明很平凡，因为 plus 的定义将 plus Z n 规范化成了 n：

plusReduces n = Refl

如果我们换种方式证明该论点，那就有点难了，因为加法是对第一个参数递归定义的。该证明同样也可以在 plus 的第一个参数 n 上递归：

plusReducesZ : (n:Nat) -> n = plus n Z
plusReducesZ Z = Refl
plusReducesZ (S k) = cong (plusReducesZ k)

cong 是库中定义的一个函数，它指明相等性也适用于函数应用：

cong : {f : t -> u} -> a = b -> f a = f b

我们可以对加法在后继上的递归行为做同样的事情：

plusReducesS : (n:Nat) -> (m:Nat) -> S (plus n m) = plus n (S m)
plusReducesS Z m = Refl
plusReducesS (S k) m = cong (plusReducesS k m)

即便对于如此平凡的定理，一口气构造出证明也有点棘手。当事情变得更复杂时，需要考虑的就太多了，此时根本无法在这种「批量模式」下构造证明。

Idris 提供了交互式编辑的能力，它可以帮助构造证明。关于在编辑器中交互式构造证明的更多详情，参见 Theorem Proving。

实践中的证明¶

证明定理的需求可在实践中自然产生。例如，在之前的视角与「with」规则一节中，我们用函数 parity 实现了 natToBin：

parity : (n:Nat) -> Parity n

然而，我们并未提供 parity 的定义。我们可能觉得它看起来会像下面这样：

parity : (n:Nat) -> Parity n
parity Z     = Even {n=Z}
parity (S Z) = Odd {n=Z}
parity (S (S k)) with (parity k)
  parity (S (S (j + j)))     | Even = Even {n=S j}
  parity (S (S (S (j + j)))) | Odd  = Odd {n=S j}

然而，它会因类型错误而无法编译：

在按照期望的类型
        Parity (S (S (j + j)))
检查 views.parity 中 with 块的右侧时

发现
        Parity (S j + S j) （Even 的类型）
与
        Parity (S (S (plus j j))) （期望的类型）
的类型不匹配

问题在于，在 Even 的类型中规范化 S j + S j 并不能得到我们需要的 Parity 右侧的类型。我们知道 S (S (plus j j)) 等于 S j + S j，但需要向 Idris 证明它。我们可以先为该定义挖一些坑（见坑）：

parity : (n:Nat) -> Parity n
parity Z     = Even {n=Z}
parity (S Z) = Odd {n=Z}
parity (S (S k)) with (parity k)
  parity (S (S (j + j)))     | Even = let result = Even {n=S j} in
                                          ?helpEven
  parity (S (S (S (j + j)))) | Odd  = let result = Odd {n=S j} in
                                          ?helpOdd

检查 helpEven 的类型会告诉我们需要为 Even 的情况证明什么：

  j : Nat
  result : Parity (S (plus j (S j)))
--------------------------------------
helpEven : Parity (S (S (plus j j)))

由此我们可以编写一个辅助函数，将它的类型重写为需要的形式：

helpEven : (j : Nat) -> Parity (S j + S j) -> Parity (S (S (plus j j)))
helpEven j p = rewrite plusSuccRightSucc j j in p

rewrite ... in 语法允许你根据相等性证明来改写它，以此改变表达式需要的类型。在这里，我们使用了 plusSuccRightSucc，其类型如下：

plusSuccRightSucc : (left : Nat) -> (right : Nat) -> S (left + right) = left + S right

我们可以在 helpEven 的右侧挖个坑来看到 rewrite 的效果，然后一步一步地做。我们从下面开始：

helpEven : (j : Nat) -> Parity (S j + S j) -> Parity (S (S (plus j j)))
helpEven j p = ?helpEven_rhs

先查看一下 helpEven_rhs 的类型：

  j : Nat
  p : Parity (S (plus j (S j)))
--------------------------------------
helpEven_rhs : Parity (S (S (plus j j)))

然后通过应用 plusSuccRightSucc j j 来进行 rewrite 重写，它会给出等式 S (j + j) = j + S j，从而在类型中用 j + S j 取代 S (j + j) （在这里是 S (plus j j)，它由 S (j + j) 规约而来）：

helpEven : (j : Nat) -> Parity (S j + S j) -> Parity (S (S (plus j j)))
helpEven j p = rewrite plusSuccRightSucc j j in ?helpEven_rhs

现在检查 helpEven_rhs 的类型会告诉我们发生了什么，包括刚才所用的等式的类型（即 _rewrite_rule 的类型）：

  j : Nat
  p : Parity (S (plus j (S j)))
  _rewrite_rule : S (plus j j) = plus j (S j)
--------------------------------------
helpEven_rhs : Parity (S (plus j (S j)))

对 Odd 的情况使用 rewrite 和另一个辅助函数，我们可以完成 parity：

helpEven : (j : Nat) -> Parity (S j + S j) -> Parity (S (S (plus j j)))
helpEven j p = rewrite plusSuccRightSucc j j in p

helpOdd : (j : Nat) -> Parity (S (S (j + S j))) -> Parity (S (S (S (j + j))))
helpOdd j p = rewrite plusSuccRightSucc j j in p

parity : (n:Nat) -> Parity n
parity Z     = Even {n=Z}
parity (S Z) = Odd {n=Z}
parity (S (S k)) with (parity k)
  parity (S (S (j + j)))     | Even = helpEven j (Even {n = S j})
  parity (S (S (S (j + j)))) | Odd  = helpOdd j (Odd {n = S j})

rewrite 的完整细节超出了本入门教程的范围，不过定理证明教程（见 Theorem Proving）中覆盖了它。

完全性检查¶

如果我们真的想要信任我们的证明，它们定义为全函数是十分重要的 — 也就是说，一个函数为所有可能的输入情况定义，并且保证会终止。不然我们就能构造出一个空类型的元素，以它开始我们可以证明任何东西：

-- 利用部分定义的「hd」
empty1 : Void
empty1 = hd [] where
    hd : List a -> a
    hd (x :: xs) = x

-- 不会终止
empty2 : Void
empty2 = empty2

Idris 会在内部检查所有函数的完全性，我们可在提示符中用 :total 命令来检查。我们会看到上面的两个定义都是不完全的：

*Theorems> :total empty1
可能不完全，由于： empty1#hd
    不完全，因为有遗漏的情况
*Theorems> :total empty2
可能不完全，由于递归路径 empty2

注意这里用了「可能」一词 — 由于停机问题的不可判定性，完全性检查当然永远无法确定。因此，该检查是保守的。我们也可以将函数标记为完全的，使其在完全性检查失败时产生编译期错误：

total empty2 : Void
empty2 = empty2

对 ./theorems.idr 进行类型检查
theorems.idr:25:empty2 可能不完全，由于递归路径 empty2

令人欣慰的是，我们在空类型一节中对零与后继构造器分立的证明是完全的：

*theorems> :total disjoint
Total

完全性检查必然是保守的。要被记录为完全的，函数 f 必须：

覆盖所有可能的输入
是良基的 — 即，当一系列（可能互相）递归的调用再次到达 f 时，它必须能够表明其参数之一已经递减。
使用的数据类型必须 严格为正（strictly positive）
没有调用任何不完全的函数

完全性的指令与编译器参数¶

默认情况下，Idris 允许所有良类型的定义，无论是否完全。然而在理想情况下，函数总是要尽可能地完全，因为这能保证它们可以在有限时间内，对于所有可能的输入提供一个结果。我们可以要求函数是完全的，通过以下两种方式之一：

使用 --total 编译器参数。
为源文件添加 %default total 指令。在这之后的所有定义都会要求为完全的，除非显式地标记为 partial。

在 %default total 声明之后的所有函数都会被要求是完全的。与此相应， %default partial 声明之后的要求则被放宽。

最后，编译器参数 --warnpartial 会为任何未声明完全性的偏函数打印一个警告。

完全性检查的问题¶

请注意，完全性检查器并不完美！首先，由于停机问题的不可判定性，它必然是保守的，因此一些 确实完全 的程序不会被检测为完全的。其次，当前实现投入的精力有限，因此它仍然有可能将不完全的函数当作完全的。你的证明请先不要依赖它！

完全性的提示¶

有时你确信一个程序是完全的，但 Idris 不这么认为，此时可以对检查器给出提示，以此来给出终止参数的详情。检查器会确保所有的递归调用链最终都能导致其中一个参数递减到基本情况，然而有些情况很难辨别。例如，以下定义无法被检查为 total，因为检查器无法确定 filter (< x) xs 一定小于 (x :: xs)：

qsort : Ord a => List a -> List a
qsort [] = []
qsort (x :: xs)
   = qsort (filter (< x) xs) ++
      (x :: qsort (filter (>= x) xs))

prelude 中定义的 assert_smaller 旨在解决这个问题：

assert_smaller : a -> a -> a
assert_smaller x y = y

它简单地求值成第二个参数，但也会向完全性检查器断言 y 在结构上小于 x。当检查器自己无法解决时，它可用于解释完全性的推理。现在上面的例子可重写为：

total
qsort : Ord a => List a -> List a
qsort [] = []
qsort (x :: xs)
   = qsort (assert_smaller (x :: xs) (filter (< x) xs)) ++
      (x :: qsort (assert_smaller (x :: xs) (filter (>= x) xs)))

表达式 assert_smaller (x :: xs) (filter (<= x) xs) 断言 filter 的结果总是小于模式 (x :: xs) 。

在更极端的情况下，函数 assert_total 能将一个表达式标为总是完全的：

assert_total : a -> a
assert_total x = x

通常，你应当避免使用该函数，不过在对原语进行推理，或者在对外部定义的，完全性可被外部参数展示的函数（例如 C 库中的）进行推理时，它会非常有用。

[1]	Timothy G. Griffin. 1989. A formulae-as-type notion of control. In Proceedings of the 17th ACM SIGPLAN-SIGACT symposium on Principles of programming languages (POPL ‘90). ACM, New York, NY, USA, 47-58. DOI=10.1145/96709.96714 http://doi.acm.org/10.1145/96709.96714